
今回は、Excelの関数を使って、ローン返済のシミュレーションを行う方法をご紹介します。
エクセルの関数と聞くと、難しそうなイメージを抱く方もいるかもしれませんが、全然そんなことはありません。理屈さえわかれば、とっても簡単です。
まずは、住宅ローンのおさらいから。住宅ローンを検討している方であれば、元利均等返済と元金均等返済という言葉を聞いたことがあると思います。
元金均等返済は、元金部分を毎回均等に返済する返済方法
名前は似ていますが、その内容は大きく違います。
元利均等返済は、言わば、元金の返済を後回しにする方法ですから、結果的に総返済額は、元金均等返済よりも大きくなります。
まあ、一方で、借り入れた当初の月々の返済額が、元金均等返済よりも少なくすむというメリットはありますが。
元利均等返済時の月々の返済額を計算する<PMT関数>
元利均等返済を選択した場合の月々の返済額を計算するには、PMT関数を用います。PMT、PayMenTの略です。ちょっと覚えにくいですね。
注意するべきところは2つです。
- 金利は、年利ではなく、月々の金利である。
- 返済回数は、借入れ年数ではなく、これも月単位である。
ですから、金利は、「年利 ÷ 12」としなければなりませんし、返済回数は、「借入れ年数 × 12」としなければなりません。
これを踏まえると、例えば次のようになります。
【年利】 2%
【返済期間】 35年
【借入金額】 3千万円
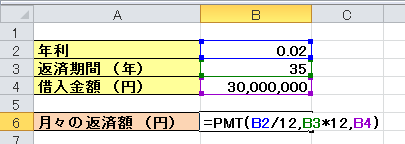


このケースで行くと、月々の返済額は99,379円になります。
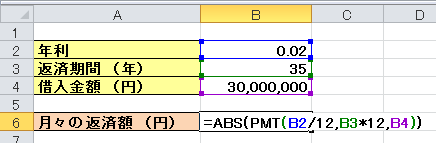
ちなみに、PMT関数を使うと、月々の返済額がマイナスの値で表示されてしまいます。プラスで表示したい場合には、ABS関数(絶対値を求める関数)で変換しましょう。
元利均等返済時の総返済額を計算する
ここまでくれば総返済額は、すぐに求められますね。
いま計算した月々の返済額に、返済回数を掛けるだけです。


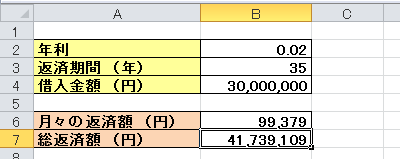
3千万円を金利2%で35年間借り入れた場合の総返済額は、41,739,109円となることが分かりました。利息分が約1,170万円です。
ちなみに、金利を3%で計算すると、総返済額は48,491,124円。利息分が約1,850万円にアップします。
住宅ローンを検討している方は、ご自分でシミュレーションすると、新しい気づきがあるかもしれません。
ぜひ、お試しください。
次回は、月々の返済額に占める、元金相当分を計算する方法をご紹介します。
<連載記事>
- 住宅ローン返済シミュレーションをエクセルで(1) <PMT関数:ローン返済額の計算>
- 住宅ローン返済シミュレーションをエクセルで(2) <PPMT関数とIPMT関数:元金返済額と利息支払い額の計算>
この記事についてのご感想などをお寄せください。
サイト運営の参考にさせていただきます。
頂いたコメントには、2〜3日以内にメールアドレス宛に回答いたします。(詳細)
メールアドレスの入力ミスにご注意ください。
なお、頂いたコメント及びその後のメール等でのやり取りは、この欄でご紹介させていただく場合がございます。